Once we acknowledge that weaving and programming are part of the same technological timeline, we can begin to look at the history of weaving as a eight thousand year long tale of human relationship with digital technologies - and use this long view to research new approaches to software engineering, a field with a much less developed history and many interesting problems to solve.

Using augmented reality to display dynamic information on a tangible programming language.
One of our threads of investigation is using the pattern matrix as a general purpose tangible programming system - one that we can use for controlling swarms of robots, programming different types of weaving systems and describing complex processes, such as live musical systems.
The magnetic system on the new pattern matrix consists of four hall effect sensors on every location you can place a block. There are four unique ways you can arrange the magnets - which means four types of programming block are possible. As we want to reuse these physical blocks for various uses and programming languages, we decided to use abstract shapes to denote the block types to begin with. Each of the four blocks can be rotated and flipped to give 32 total possible orientations, or symbol 'tokens':
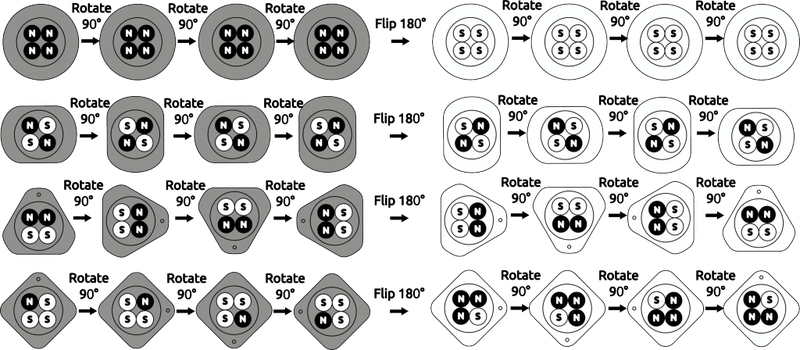
All combinations of token orientation with four magnets
However, only 16 of these orientations are actually unique. We can only determine flip orientation on the circular block, and only rotation on the rectangular and triangular ones - where flipping them makes no difference to the magnets. The square block is a kind of special one, as we can tell both rotation and flip orientation, so it can represent eight tokens in total all by itself:

All unique tokens and orientations possible.
With mid-grey shapes the flip (which side is up) is irrelevant. It's important to note at this point that the parallels with tablet weaving are no coincidence: rotating and flipping arrangements of four binary elements for this magnetic system are the same actions as those performed when weaving using tablets. Weaving in the pattern matrix is more than a subject, it's built directly into it's mode of operation.
Next we need to test the applicability of this tangible programming system for wider uses. The other cultural phenomena the Penelope project is involved in is livecoding - so is it possible to use the pattern matrix to introduce a weaving centred programming technology in a very different context, not to describe weaving but to generate music in a performance such as an Algorave? This is something that Ellen first pioneered at our weavecoding performance at The Museum of casts of classical sculptures in Munich, but the new pattern matrix has better capabilities for a general purpose programming language.
Having 16 states of four blocks is indeed limiting for a language, but not too limiting. Some types of programming language, such as a string rewriting system like a Lindenmayer system are particularly well suited to this. They are also surprisingly Turing complete languages, able to represent any other programming language in existence, given enough space and time.
Here is a quick example of how this works in text form - a string rewriting system is simply a list of search-replace actions that are carried out in a consistent order. The original example, used to model the growth pattern of algae - consists of a starting string: "A" and two replacement rules, replace "A" with "AB" and replace "B" with "A". If we run these two rules over and over on the same bit of text we gradually 'grow' a pattern like this:
n = 0 : A
n = 1 : AB
n = 2 : ABA
n = 3 : ABAAB
n = 4 : ABAABABA
n = 5 : ABAABABAABAAB
n = 6 : ABAABABAABAABABAABABA
n = 7 : ABAABABAABAABABAABABAABAABABAABAAB
On the pattern matrix we use four of the rows to represent four different rules that replicate in this manner (each made of 5 possible symbols, as it's a 5x5 grid), which we run 8 times on the starting string (A) to create a musical sequence. Four of the tokens represent these rules (A,B,C and D), the remaining tokens represent musical actions - changes in pitch, rests and sound triggers. There is massive variety of potential patterns, you can control the amount of recursion by the number of rule reference tokens you use - to control the resulting length of the sequences, and thus the complexity of the music. Interestingly we also need a 'no operation' (NOP) instruction that does nothing - as in low level assembler languages. We need this as a way to be able to shift timing in the musical sequence by one instruction.
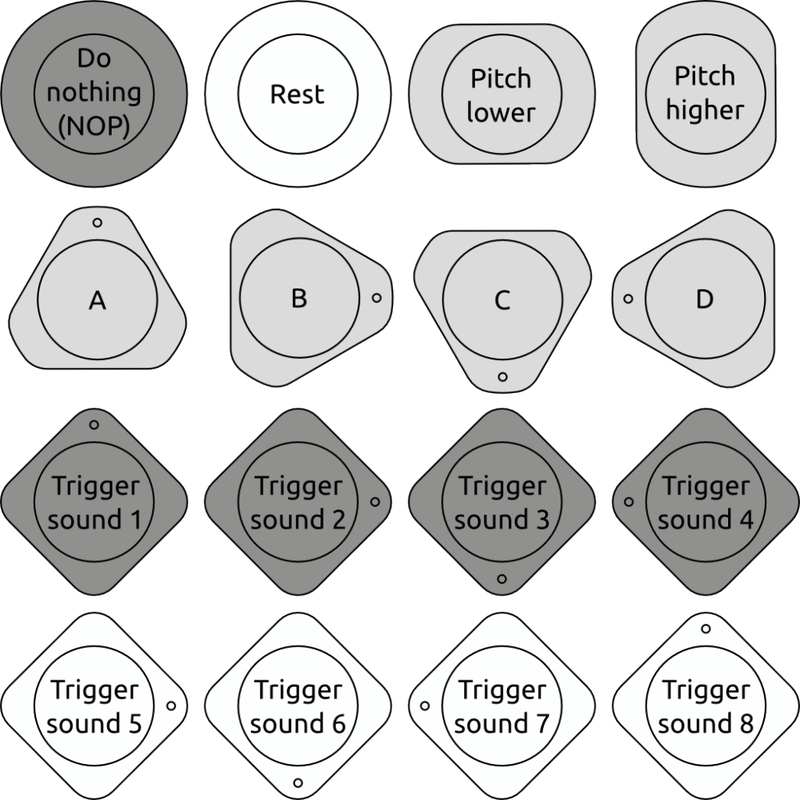
A musical language in 16 instructions.
With a tangible programming language like this it's also very important to consider how you categorise instructions by shape - as you can quickly switch between similar operations by simply rotating or flipping tokens, while switching between different shapes takes longer (as you need to pick up a new block) so should represent bigger changes if possible.
Four rules are plenty for generating hugely complex sequences, so we can use the fifth bottom row to control global parameters like scale, synchronisation options (for our slub collaborative sync protocol) or switch between more banks of sounds for greater variety.

Slub performance including the pattern matrix at the Brighton British Science Festival Algorave
The first time we tried this out was at the British Science Festival Algorave in Brighton. A projection was set up with a camera to show the pattern matrix being used, and while technically everything went fine (other than some syncing difficulties), it highlighted a key problem with tangible programming languages. With no dynamic feedback other than the state of the blocks on the pattern matrix, it's very difficult to tell what is happening during a performance, it's hard to understand what musically is resulting from the changes you are making.
In order to find a way around this we designed an augmented reality 'layer' to place over the pattern matrix, which gives feedback on the currently triggered notes and the paths between the recursive string production rules. We use fluxus and it's AR feature, which was written by Gabor Papp - which is based on the ARToolkit library. We use a printed out marker to find the plane and camera scale of the centre of the pattern matrix in the image from a USB camera. Once this is done the marker can be removed (as neither the camera or pattern matrix moves) and we can use millimetres as units and place objects over the block locations in 3D space. When the sensors detect a change we can display this new information, also updating the current position in the sequence playback to give feedback on the current sound playing.

Pattern matrix livecoding as part of slub performance at the Algomech Algorave. Pix thanks to Dan Hett
As an initial trial the AR improved things when first tried out at the Algomech Algorave in Sheffield, it makes the pattern matrix easier to understand and perform with - and also provides some feedback for the audience in a projection. In a last minute change we switched from Latin characters to Linear A, an undeciphered ancient Greek script - a reference to Flavia's work on the Penelope project. This is actually preferable to Latin characters as the musical language represents meaning in a way that that actual glyph used is irrelevant - it's better if it can't be 'read' or confused with another meaning by anyone (still alive).
So it seems that AR could be one of the items in our toolbox for further tangible programming experiments. Perhaps we can better explain the structural changes caused by livecoding the weaving notation for the warp weighted loom by having a dynamic weave structure 'floating' on top of the tokens, alongside the loom simulation. This could also be of use for describing tablet weaving actions with these blocks, which would need to be more abstract than the binary weaving notation.
Another area to explore is the design of the blocks themselves, moving away from the abstract shapes, we can design them for specific purposes. Similar to our work on viruscraft, where we have more closely explored the correspondence between physical form (receptors and structural protein arrangements) and tangible interfaces, it seems that these shapes may be worth considering more closely now the sensor matrix is working well.
